圆桌会议

                                                                Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)

                                                                                    Total Submission(s): 6281    Accepted Submission(s): 4334

Problem Description

HDU ACM集训队的队员在暑假集训时经常要讨论自己在做题中遇到的问题.每当面临自己解决不了的问题时,他们就会围坐在一张圆形的桌子旁进行交流,经过大家的讨论后一般没有解决不了的问题,这也只有HDU ACM集训队特有的圆桌会议,有一天你也可以进来体会一下哦:),在一天在讨论的时候,Eddy想出了一个极为古怪的想法,如果他们在每一分钟内,一对相邻的两个ACM队员交换一下位子,那么要多少时间才能得到与原始状态相反的座位顺序呢?(即对于每个队员，原先在他左面的队员后来在他右面，原先在他右面的队员在他左面),这当然难不倒其他的聪明的其他队友们,马上就把这个古怪的问题给解决了,你知道是怎么解决的吗?

 

Input

对于给定数目N(1<=N<=32767)，表示有N个人,求要多少时间才能得到与原始状态相反的座位顺序(reverse)即对于每个人，原先在他左面的人后来在他右面，原先在他右面的人在他左面。

 

Output

对每个数据输出一行，表示需要的时间(以分钟为单位)

 

Sample Input

4

5

6

 

Sample Output

2

4

6

看到这道题我先是画了前两个标准输入的图，然后以为就是将数值去掉开头和结尾然后进行冒泡排序。结果是我错了，不过思路是对的，只是还差了一点。首先题目条件是1个圆，求的是使与原始座位相反所要移动的时间。那么他就不需要从头到尾全部变成反的。移动次数，也就是移动时间最少的方法其实是，把圆桌砍成两个半圆，两个半圆分别将座位顺序变成相反那么如下图所示，我只画了一半的变换，红色代表的是变换位置的两个人。总的变换次数，也就是变换时间就是左边的冒泡排序复杂度加上右边的冒泡排序复杂度。sum=（n1-1)*n1/2+(n2-1)*n2/2;

 

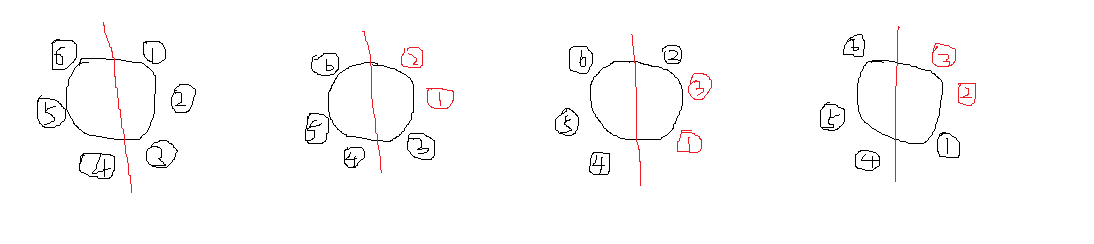
ac代码：

#include
       
        using namespace std;int main(){    int n;    while(cin>>n){        int n1,n2;        int x;        n=n+1;        if(n%2==0){            n1=n/2;            n2=n1-1;        }        else{            n1=n2=n/2;        }        x=n1*(n1-1)/2+n2*(n2-1)/2;        cout<
        
         <